How to teach numbers

In primary school we are taught to count using our fingers and that numbers are supposed to be written using our very cleverly devised system. In this post I propose a somewhat different approach.

Our way of writing down numbers is quite well designed. It allows for some very clever tricks when performing simple algebraic computations.

For example, long multiplication and long division are a very handy side-effect of our number system. Unfortunately our first introduction to numbers is usually accompanied by a lengthy explanation of all the clever tricks that can be used to quickly compute the value of simple expressions. Our teachers get so caught up in teaching those clever tricks that they forget to teach the most fundamentally important concept in elementary mathematics: Asking questions.

In what follows, I will explain numbers and how elementary algebra is just fancy counting. I will deliberately focus on the meaning of operation rather than on how to practically compute the result.

Back to the basics

Dots on a line

There's no need to start with an abstract definition of a number. Instead, draw a line with an ellipse on one end. Now draw some dots on that line approximately equal distances apart.

This ellipse happens to be called 'zero'. Numbers are about asking the question "How many steps away from zero is this dot?".

After the first step we are at one, after another step we find ourselves at two and after one more step we arrive at three.

To be honest, the way we name and write down numbers already seems way more confusing than the numbers themselves. The symbols are arbitrary and the names even more so, but we know how to count, so let's start counting.

Addition and subtraction

Let's take an example. If we start at zero, take three steps to arrive at $3$, then take five more steps in the same direction, we arrive at a dot that we label $3 + 5$. We pronounce $3 + 5$ as 'the sum (or addition) of $3$ and $5$'.

Note that the counting happened before the labeling. Addition is just the name for this way of counting.

The addition, the number with label "$n + m$", of two numbers $n$ and $m$ is all about the following question:

"If I'm at $n$, then take $m$ steps in the direction away from zero, where do I end up?"

If we go about it the other way around, and take $5$ steps first, then $3$ more steps, we arrive at a dot that we would like to label $5 + 3$. However, we notice that it's already labeled $3 + 5$. Similarly, if we just take $8$ steps starting from zero, we arrive at that same dot as well. This is why we state that $3 + 5$ equals $8$, as well as $5 + 3$.

Again, note that we start with the process and conclude that 8 equals $3 + 5$, not the other way around. In the case of numbers, 'equals' just means 'using these two different ways of counting, we arrive at the same dot.'.

Let's take another example. If we start at $8$ and step backwards for $3$ steps, we end up at a number that we label $8 - 3$. This number happens to be $5$. In other words, to get to $8$, starting from $5$, it takes us $3$ steps. That's why we say $8 - 3$ equals $5$. This label $8 - 3$ is called the subtraction of $3$ from $8$.

The subtraction $n - m$ of two numbers, $n$ by $m$, requires the following question:

"If I'm at $n$, then take $m$ steps back into the direction of zero, where do I end up?"

or, alternatively:

"If I'm at $m$, how many steps do I have to take to get to $n$?"

Multiplication

Up until now we've only ever taken one step at a time. Steps of plus one, if you will. Let's see what happens if we take bigger steps.

Suppose we are at zero and start taking steps away again. This time, however, instead of taking steps of plus one, we take bigger steps, say steps of plus two, for example. After one big step of plus two we arrive at two. After another such step we are at four and one more step later we get to six.

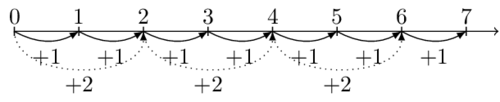
Because it takes $3$ steps of $+2$ to get to $6$, we say that $3 \times 2$ equals $6$. Incidentally, taking $2$ steps of $+3$ also gets us to $6$.

Now it's easy to see that taking no steps of arbitrary size gets us nowhere. We would just stay at zero doing that: $0 \times anything = 0$. Similarly, taking any number of steps wherein we don't move forward at all, gets us no further either: $anything \times 0 = 0$.

The multiplication $n \times m$ of two numbers $n$ and $m$ is about asking the following question:

"If I take big steps of size $m$, where do I end up after $n$ of such steps?"

If we describe this 'taking steps of $+something$' behavior can be described as 'living in a $+something$ system'. In a $+something$ system, we can only take steps of $+something$.

Now we can ask the question of the multiplication of $n$ and $m$ in terms of such a system:

"In a system of $+n$ steps, where do I end up after $m$ steps?

Division

Let's say we are back in this $+2$ system. We can only take steps of $+2$. How many steps does it take to get to $8$? As we saw in the previous section, we need $3$ steps of $+2$ to get to $6$. One more step of $+2$ then gets us to $8$ so it takes $4$ steps of $+2$ to get to $8$.

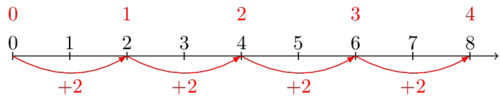
Because it takes $4$ steps of $+2$, we say $8 \div 2$ equals $4$.

Because it takes no steps of arbitrary size to get from $0$ to $0$, we say $0 \div anything = 0$.

Now comes the striking idea of division by zero. Let's see if you can figure out why division by zero has no good answer.

It takes $3$ steps of $+4$ to get to $12$, so $12 \div 4$ equals $3$, but how many steps of $+0$ do we need to get to $12$? In other words, what is $12 \div 0$? There is no number of steps of size $+0$ that you could ever take to arrive at $12$, so we say $12 \div 0$ is undefined. Similarly, $anything \div 0$ is undefined.

Undefined, in the case of numbers, just means 'there is no good answer to the question that these symbols represent'.

Division is to Multiplication as subtraction is to addition. As such, the division (or quotient) $n \div m$ of a number $n$ by another number $m$ is about asking the following question:

"How many steps of $+m$ does it take to get to $n$?"

or, alternatively, using the system explanation:

"In a $+m$ system, how much is $n$?"

You see, $8$ is $4$ if you are counting in $+2$-sized steps and $12$ is $3$ in a $+4$ system.

You could say that $4$ is $4$ in a $+1$ system. Similarly, $9$ is $3$ if you are counting in a $+3$-sort-of-way.

Pause to breathe

At division is where most people stopped trying to push elementary mathematics into their brains. I challenge the idea that not everyone can understand the basics. As I said, it's all about questions. A curious student will, at this point, have started to ask more of their own questions.

"Why not continue this trend of changing systems?" "What happens if I take different kinds of step?" "Do I have to take equally large steps every time?"

That's exactly where the next part takes off.

Powers

Up until now, we have only taken steps of $+something$. We know what multiplication is now, so let's try taking steps of $\times something$.

You'll notice you won't get very far if you start at zero, so we'll have to start from somewhere else. How about one? Let's draw that line again:

Let's look at a system of $\times 2$.

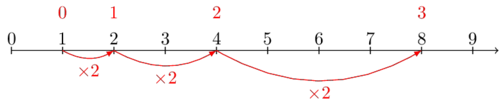
After one step, we're at $2$. After two steps, we find ourselves at $4$. The third step(power) brings us to $8$.

The idea that steps of $\times 2$ are somehow 'larger' can be misleading. They are just a different way of counting. As such, we can draw this line with the dots placed in such a way that the steps seem equal in size.

This makes it easier to simply think of them as different steps.

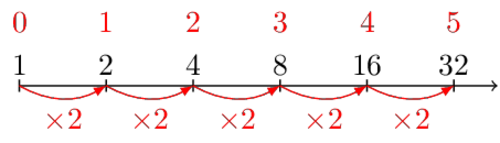
After two steps of $\times 3$, we are at $9$. This is why we say that the second power of three ($3^2$) is $9$.

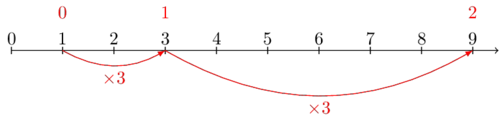
Finding $n^m$, the $m$-th power of $n$, is about asking the following question:

"In a $\times n$ system, where do we end up after $m$ steps?"

Logarithms

Now for the operation that looked like alien magic the first time we looked at it: logarithms.

Let's start with an example. If we take $3$ steps of $\times 2$ and end up at $8$, that means it takes $3$ steps of $\times 2$ to get to $8$.

How many steps of $\times 3$ does it take to get to $9$? Well, just count them. We need to take $2$ steps of $\times 3$ to get to $9$.

$9$ is $2$ in a $\times 3$ system. $8$ is $3$ in a $\times 2$ way of counting. $4$ is $2$ in a $\times 2$-sort-of-way.

We can write it down as follows:

$$ {\text{counting in}}_{\text{ a } \times 2 \text{ system }} 8 = 3 $$

or, shorter:

$$ {\text{counting in} \times}_{2} 8 = 3 $$

We call this concept a logarithm and write it down as follows:

$$ {\log}_{2} 8 = 3 $$

Because $2^3$ equals $8$, we say that the logarithm, in a $\times 2$ system, of $8$ is $3$. Because $2^3$ equals $8$, we say that the logarithm, base $2$, of $8$ is $3$.

How many steps of $\times 5$ does it take to get from $1$ to $1$? Zero steps. We say that $\log_{5} 1$ equals $0$. Similarly, $\log_{anything} 1$ equals zero.

How many steps of $\times 0$ does it take to get to $7$? You can take any number of steps of $\times 0$, but you will never move go anywhere except to $0$. As such there is no number of steps that you could take to get to $7$ in a $\times 0$ system. We say $\log_{0} whatever$ is undefined.

Now we will investigate why there was no way to put $0$ on the 'log' scale we drew earlier. To plot $0$, we would have to count how many steps, forwards or backward, of size $\times 2$ we would have to take to get from $1$ to $0$. Because no number of steps suffices to get to $0$, we say that $\log_2 0$ is undefined. Similarly $\log_{whatever} 0$ is undefined. This is why we cannot plot $0$ on a log-scale.

Computing $\log_{n}{m}$ is about asking the following question:

"How many steps of $\times n$ does it take to get to $m$?"

or, alternatively:

"In a system of $\times n$, how much is $m$?"

Square Roots

Roots are the most confusing of the elementary operations in my opinion.

Now we're going to look at things that are $2$ in a $\times something$ system. 4 is $2$ in a $\times 2$ system, $9$ is $2$ in a $\times 3$ system, $16$ is $2$ in a $\times 4$ system. Things that are $2$ in a $\times something$ system are called squares and their systems are called the square roots. That means that $4$ is a square with square root $2$, $9$ is a square with square root $3$ and $16$ is a square with square root $4$.

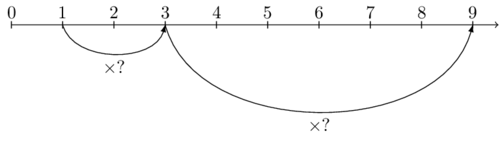
If it took me two steps in a $\times$-something system to get to $9$ so they must have been $\times 3$-steps.

If $16$ is $2$ in a $\times$-something system, then it must have been a $\times 4$ system because $1 \times 4 \times 4$ equals $16.

Computing $\sqrt{n}$ is about asking the question:

"If I know I took two steps in a $\times$-something system to arrive at $n$, how big were my steps?"

Conclusion

Numbers don't have to be confusing. You just need to learn to ask the right questions and stay curious.

If you liked this explanation, and there is some other bit of mathematics that you would like explained, please let me know. I love explaining maths to people who really don't like maths (yet).