A base n numeral system

I've heard a few people suggest that mathematics is not something universal. One argument I heard is that "one plus one is two for us, but it doesn't have to be that way.". If you don't see what's wrong with that argument immediately, have a look at the definition of our numbers.

It's true that the way we write our numbers is not universal. This becomes clear immediately when we look at other numeral systems. If you've heard about binary digits, you know that we can write numbers in different ways. Usually a way of writing numbers is specified so that basic operations such as addition, subtraction and comparison of size are easily carried out.

A programmer's view

You can imagine numbers as dots on a line. No matter how we name these dots, they're still the same dots. The way we write numbers is just a way of naming those dots.

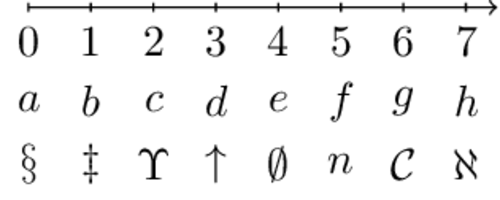
A number line with completely different signs

To get a programmer's taste of how numbers are universal, I'll define a base $n$ number system. Programmers use this kind of reasoning in a number of ways. Only one of those is to prove that a particular set of objects is countable. If we can write every element of the set as a number in a specific numeral system, we know the set is countable.

The value of a number

Let's have a look at how we write numbers. $495$ means $4$ times $100$ units plus $9$ times $10$ units plus $5$ units.

In general, if $d_{i}$ denotes the $i$-th digit of a $k$ digit number in a base $n$ system the value of the number is calculated as follows:

$$ (d_{1}d_{2}\dotsc d_{k}){n} = \sum{i=1}^{k}n^{k-i}d_{i} $$

We don't need to write numbers in an ordered fashion like this, but this is the way we do it and this way has some nice properties:

We can get an idea of how big the number is by looking at how many digits are needed to represent it.
Once we know how to write all the digits, we can write down the representation for any number.

There are also some advantages for programmers:

We can perform addition and subtraction in logarithmic time with respect to the value of the numbers.
We can perform multiplication and division in a logarithmic amount of additions with respect to the value of the numbers.
We can perform exponentiation in a logarithmic amount of multiplications with respect to the value of the exponent.

For an arbitrary number system, here is a function that gives the value of a representation of a number.

import Data.List (elemIndex)

value :: Eq a => [a] -> [a] -> Int
value system [] = 0
value system (d:ds) = case elemIndex d system of
    Nothing -> error "unrecognised digit"
    Just dv -> (dv * n ^ length ds) + value system ds
    where n = length system

Prelude> value ['0'..'9'] "56"
56
Prelude> value ['a'..'z'] "cssyd"
1243115

The written representation of a number

The conversion from one number system to another usually consists of finding the value of a number and then building a representation for it in the other system. In the previous paragraph, you saw a formula to find the value of a number given its representation. Suppose you have a number of value $v$, how to we build a representation for it?

The amount of digit in the representation of a number is equal to the number of times it can be divided by the base before resulting in zero. The remainder of this devision is then the index of the digit in the numeral system of digits.

representation :: [a] -> Int -> [a]
representation system value | value < n = [system !! end]
                            | otherwise = representation system start ++ representation system end
    where                    
        start = value `div` n                           
        end   = value `rem` n                           
        n     = length system  

Prelude> representation ['0'..'9'] 56
"56"
Prelude> representation ['a'..'z'] 4657
"gxd"

It is important to note that we can use any type of element for the digits of the number system, not just characters. The resulting representation is an ordered list of those elements.

To really show you that these lists of digits are well defined representations of numbers, let's instantiate the Num type class.

system = ['a'..'z']
instance Num String where
    s1 + s2 = representation system $ value system s1 + value system s2
    s1 * s2 = representation system $ value system s1 * value system s2

Prelude> "cs" + "syd"
"tav"
Prelude> "cs" * "syd"
"byyyc"

Hopefully by now, you've been convinced that numbers are not constructed by humans. Only the way we represent them is.